I saw that, 170 kts / MACH 0.40. That’s a clever way to preserve climb performance, I have flown turboprops without MACH meter on which the normal climb schedule was 160 kts to FL150, then reducing 3 kts every 1000 ft until reaching FL250 at 130 kts to preserve climb performance, its basically the same as changing over to MACH (just calculated it, in ISA its the same as changing over to M 0.32). Although the reduction in IAS / CAS by flying a constant MACH number does not exactly relate to the speed at which you’ll find the highest excess power (best climb rate), I guess its a good compromise.
How are you calculating that??? The speed of sound in air is totally dependent on temperature - that is the only variable in the formula. 170/0.4 is 425 knots. The colder the air, the slower sound travels, and the coldest temperature ever recorded on Earth stands at -135°F recorded in Antarctica. At that temperature, sound still travels at 523 knots.
By the way, the formula for calculating the speed of sound in knots according to temperature is:
V=644*√(1 + T/273.15) where T is the temperature in Celcius.
170/0.4 isn’t a calculated value. These are simply the climb speeds from the 930 PIM.
Most, if not all high performance aircraft have the climb speeds in IAS and Mach.
After having a look at the charts, I think what they’re saying is max climb should either be 170 indicated or M0.4, whichever is less. So I decided to see if I could actually get those #'s on the screen at the same time. I had to go to McMurdo Station to do it, but I actually did it. And I don’t know if I should be shocked or not, but 236 KTAS (170 KIAS) at -55°C actually works out to .410 Mach, which was displayed on the PFD. At least that’s something that’s right, whether it’s from Asobo or WT. It took starting out at -32°C on the ground to get those #'s though, so I doubt I’ll ever see them again.
This has nothing to do with temperature. There’s always an altitude where e.g. 170 and 0.4 match.
That’s the crossover altitude.
When you are climbing at a constant IAS, Mach number increases.
As soon as IAS matches Mach, you continue to climb with Mach (and IAS will continuously decrease).
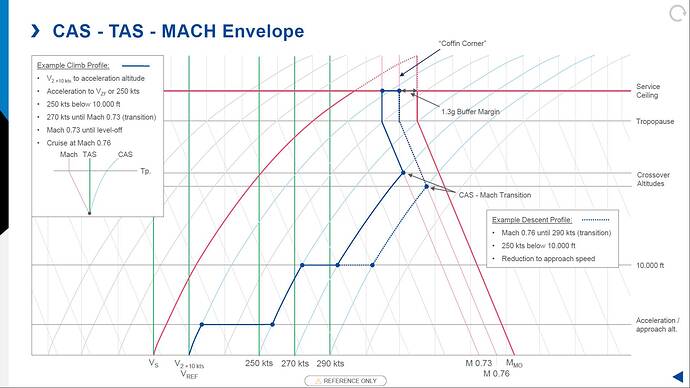
Meaning 170 kts indicated / calibrated up to crossover altitude (reaching M 0.40) then M 0.4 above. By the way, I have taught aerodynamics to ATPL students, I’m well aware how to calculate the LSS.
Its easier to use 38.94 x square root of the temperature in K (C + 273).
What I’m saying is that if you start somewhere that’s reasonably warm, you’ll never see temps at altitude that are cold enough for that. The warm air (relatively speaking) will keep the speed of sound high enough that your Mach # will never reach 0.4.
Are you sure? In ISA crossover from 170 kts CAS to MACH 0.40 happens around 23000 ft pressure altitude already. I think you are forgetting that the TAS increases when climbing at a constant CAS. MACH number = TAS / LSS. So you can increase the MACH number by either increasing the TAS or reducing the LSS (or both). During climb both TAS increases and LSS decreases (LSS decreases up to the tropopause at which temperature is isothermal and therefore LSS remains constant with increase in altitude).
How did you come up with that number? In your calculation LSS (M1.0) = 1063 kts?! To prevent any confusion, all jets and some turboprops have a climb schedule consisting of a Calibrated Airspeed (CAS), changing over to a MACH number. When continuing to climb at a constant CAS the MACH number keeps increasing until exceeding the Maximum Operating Speed in MACH (Mmo), which is the point the airflow over the wings reaching the speed of sound.
Instead climb is initiated at a certain CAS (example 170 kts), at a certain point during climb (crossover altitude) the climb MACH is reached (M 0.4 on the TBM) and climb is continued at constant MACH number instead. In case of TBM I assume this is done to preserve climb performance rather than reaching Vmo/Mmo, at least that was the case on turboprops I have flown.
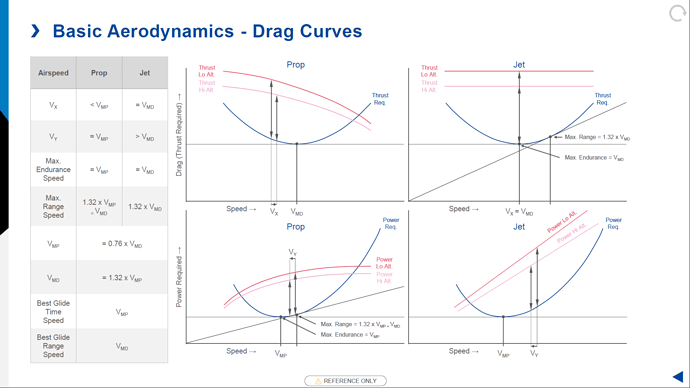
During climb the speed at which maximum excess power exists (or any excess power at all) reduces during climb so it would make sense to reduce speed at a certain point to maintain a positive rate of climb. Should you be interested, below the drag and power curves for a prop illustrated. You can see the Vy decreasing with increase of altitude while Vx increases, Vx = Vy at the aircraft theoretical ceiling. You can also see the speed at which there is excess thrust or power decreasing with altitude.
As @anon50268670 mentioned, the ISA deviation e.g. at FL300 will never be sufficient for this to happen.
Well, I stand corrected. I took off out of Pecos Texas with 38°C on the ground. With 95% torque, I kept the FLC at 130 up to about FL200, then raised it to 170 KIAS. The Mach indicator took longer to activate (M0.3 minimum), but it finally came in about a minute later. At about FL270, it was finally cold enough outside for my Mach # to hit 0.39, and I hit the SPD button to hold that.
In other words, 170 divided by 0.4 is 425. At that point, I did not yet realize that it was an either-or thing and that what was being said was 170 KTAS was actually M0.4. My point was that in order for that to be true, then the speed of sound would only be 425 knots, and that there is no place on Earth cold enough for that to happen. In fact, it would have to be -154°C (-245°F) in order for that to happen.
By the way, I sourced my original formula from the link below. Where my velocity constant is 644 for knots, theirs is 331.3 to result in m/s. If you multiply that by the conversion factor for m/s > knots, you get 643.99 - I rounded up.
Usually you keep one climb schedule, either 124kias or 170kts/M0.4.
If you change it, it makes only sense the other way round.
High speed at low altitude and if climb performance starts to drop you switch to the low speed schedule.
Not only is it cold enough, lowering the LSS sufficiently. Also the TAS increased sufficiently to reach the respective MACH number:
LSS at SL (ISA) = 661 kts
LSS at 27000 ft (ISA) = 596 kts
Difference = -65 kts
TAS at SL (ISA) = 170 kts
TAS at 27000 ft (ISA) = 259 kts
Difference = +89 kts
I think 38.94 x square root (C + 273) is further simplified, its the most common used formula to calculate LSS in aviation, its in all ATPL textbooks at least. Should give the same result.
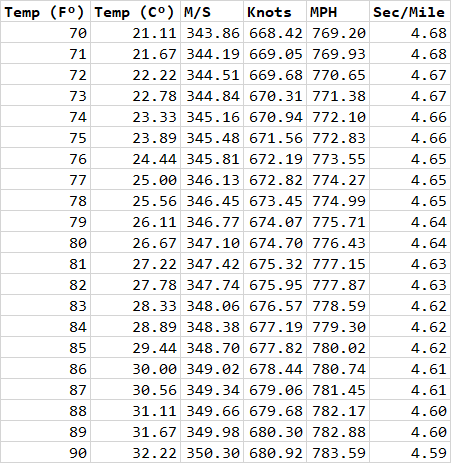
The formula really doesn’t matter to me, as long as it yields the right output. I actually have a spreadsheet that I use during thunderstorms to determine lightning distance. Miles per hour can be converted to seconds per mile by dividing 3600 by MPH. Since temp is the determining factor, this was the easiest way to get what I needed. Here’s a snippet:
Of course, once I saw that the range was pretty small for the temps normally seen in a thunderstorm, I just started using 4½ seconds as a general rule. It gets me close enough.
I like to lower my nose a bit before my cruise altitude just to start gaining some ground horizontally. Higher ground speed means getting there quicker. I find it to be a decent compromise between getting into the higher/thinner air to save fuel and actually getting where I’m going as quickly as possible. And yes, this might not be “by the book,” but it’s how I like to do it.
I think the 170 kts / M 0.4 profile is doing just that. Its a compromise between ground distance covered and maintaining acceptable climb performance. I don’t think you will cover more ground climbing with 124 kts first, then increasing to 170 kts versus climbing with 170 kts all the way.
According TBM 930 POH:
Climb with 124 kts to FL200, then 170 kts / M 0.4 to FL300
- Time: 15:15
- Fuel: 54 kgs
- Distance: 47 nm
- Average TAS = 185 kts
Climb with 170 kts / M 0.4 all the way to FL300:
- Time: 17:15
- Fuel: 62 kgs
- Distance: 62 nm
- Average TAS = 216 kts
If you take the difference in distance covered between climbing with 170 kts / M0.40 all the way and your technique and calculate the fuel consumed using the TBM recommended cruise technique you’ll consume 8 additional kgs to cover the same distance as climbing with 170 kts / M 0.4 all the way. Total difference in fuel consumed therefore is 62 - (54 + 8 ) = 0 ![]() .
.
In other words it would only make sense to use 124 kts (best rate) for terrain / obstacle clearance or ATC request. The Specific Fuel Consumption (SFC) is important which is the fuel flow divided by distance covered, most aircraft have an optimized climb schedule to achieve optimum SFC, the 170 kts / M0.40 climb profile does exactly that.
Don’t try to outsmart the manufacturer ![]() .
.
That’s what I thought - get into the thin air faster and save go-juice, but get there slower - or cover more ground while burning fuel in the thicker air. I figure I’m splitting the difference - getting into thinner air so that it doesn’t cost as much to get more ground speed before leveling out.
I kinda figured it would break even either way. Thanks!