Welcome to the forum! We had the same discussion some time ago in another thread. It seems you have a good understanding regarding TAS versus CAS. Your question goes a little deeper as your observation is about Vmo (maximum operating speed in kts) versus Mmo (maximum operating speed in Mach). I added TAS → Mach relationship to the already long explanation about speeds, I hope its not too much, guess you can skip right to the end if IAS → CAS → TAS is clear already:
Types of Airspeed
To start there are different airspeeds:
- Indicated Airspeed (IAS) is the airspeed measured by the airspeed “sensor” (called pitot probe).
- Calibrated Airspeed (CAS) is the IAS corrected for errors in measurement and instrument errors, on modern aircraft this is the airspeed displayed on the speed tape.
- True Airspeed (TAS) is the CAS corrected for air density.
- Groundspeed (GS) is the TAS corrected for wind and is the speed the aircraft is actually travelling over the ground.
Then we didn’t take into account Equivalent Airspeed (CAS corrected for compressibility when flying at higher MACH numbers) and MACH, but that is for another day maybe…
IAS → CAS
IAS to CAS is generally only a few knots, not very significant. Modern aircraft with Air Data Computers automatically correct for this and CAS is displayed on the speed tape. On small GA aircraft you’ll need to correct for position and instrument errors according to tables published in the aircraft POH.
CAS → TAS
Density has much bigger effect on airspeed, the airspeed indicator is calibrated according International Standard Atmosphere (ISA), therefore: CAS = TAS only at sea level and in standard atmosphere. In other words, whenever the air density is different than the air density on a “standard day” at sea level the TAS differs from the CAS. The density of the air is depending on:
- Air pressure
- Air temperature
- Humidity
In Mickey Mouse language: If air density decreases, an aircraft needs to fly faster (true airspeed) to encounter the same amount of air molecules per time frame (indicated airspeed) in order to produce the same amount of lift on the wings. Commercial aircraft flying at FL300 and higher therefore have a considerably higher true airspeed compared to the speed displayed ont the speed tape. By the way True Airspeed, Ground speed and MACH number are often displayed somewhere on the PFD and / or ND as well.
Why isn’t TAS displayed on the speed tape instead of the CAS? Aircraft performance, lift produced by the wings etc. is directly related to the CAS rather than TAS. As an example, the aircraft stall speed given as a CAS does not change with change in air density. Stall speed given as a TAS does vary with air density and it is therefore not practical to fly using TAS. We usually calculate the TAS as an intermediate step in calculating the aircraft groundspeed (taking into account the wind) and MACH number. Otherwise TAS does not serve a practical purpose during flight.
Kinetic Energy
Maybe it goes too deep into the weeds. CAS is an indication of the kinetic energy, the lift created by the wings is depending on the kinetic energy of the air passing over it (amongst other factors such as wing area for example). Kinetic energy of an object is calculated by the formule K = 1/2 x M x V2 in which M is the mass of an object and V is the speed of the object.
Its a little difficult to determine the kinetic energy of air passing over the wings as it is not an object which you can simply put on a scale and measure its mass. For the purpose of lift and aircraft performance we calculate the kinetic energy by replacing the M (mass) in the formula by air density (mass of the air per square meter), the letter P (Greek letter “rho”) is commonly used to indicate this.
Relationship CAS, TAS & Density
So: CAS = 1/2 x P x V2, the V in the formula is the TAS. You can see with a simple example that for a constant CAS on the speed tape, TAS differs depending on the density of the air. For a CAS of 10 and an air density of 1, the TAS needs to be 10 as well:
At sea level on a standard day: 10 = 1 x 10
If we now climb at a constant CAS, air density reduces as we climb higher. If we take an air density of 0.5 for example TAS would be 20:
At higher altitude: 10 = 0.5 x 20
Those are of course completely made up numbers and we took the constant out of the equation so its only for illustrative purposes. I hope it at least shows the relationship between CAS and TAS and air density. I tried to keep it simple, I hope I somewhat succeeded 
 .
.
TAS → Mach
Local Speed of Sound - The Local Speed of Sound (Speed of sound in TAS) reduces with reducing temperature as you climb. The LSS can be calculated by:
- LSS = 38.94 * square root of temperature in K (C + 273).
Mach number - The aircraft MACH number is the aircraft speed (TAS) in relation to the local speed of sound, the Mach Number can be calculated by:
As all current airliners (Concorde was an exception) are designed for subsonic flight only, the Maximum Mach number is generally somewhere between M 0.80 to M 0.90 (80 to 90% the speed of sound), above this speed the airflow on top of the wing will reach the speed of sound and causes shock-waves to form which cause the airflow to separate and wing to stall, Mach tuck causes the nose to lower and the speed to increase even further, aggravating the situation. In short, on an airliner you don’t want the airflow on top of the wings to go supersonic.
When climbing at a constant CAS as we normally do at lower altitude, both the TAS increases as explained above and the temperature, and thus the local speed of sound decreases. Since the Mach Number = TAS / LSS, TAS goes up and LSS goes down (getting closer together), I hope you understand the Mach number increases during climb at constant CAS. If we would continue to climb at constant CAS we will eventually exceed the Mmo. This is the reason you see your max. speed on the speed tape reducing with increase in altitude!
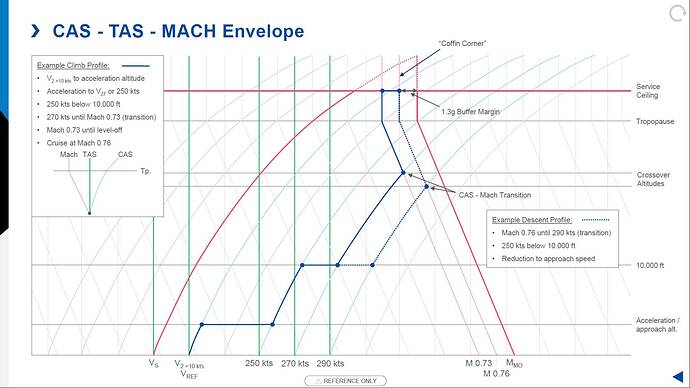
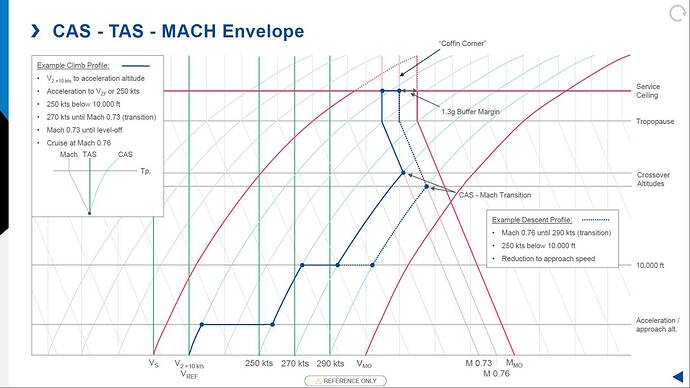
At some point you’ll need to change over from constant CAS climb to constant Mach climb, this altitude is called the “crossover altitude”. In the graph below you can see the relationship between CAS, TAS and MACH illustrated.
- CAS - The curved lines are CAS, following a curved line you can see the TAS (straight lines) increasing and so does the MN (diagonal lines which become straight at te Tropopause).
- TAS - similarly when following any straight (TAS) line you can see the CAS decreasing and MN insreasing.
- MACH - The diagonal line are Mach numbers, those lines reduce until reaching the tropopause. As the temperature at the tropopause remains constant with increase in altitude, the LSS stops reducing and therefore for the line starts to follow the TAS (straight) lines.
If you continue climbing you will eventually reach a point where the low speed stall and high speed stall intersect. Theoretically if you decelerate 1 kt the aircraft will enter an aerodynamic stall, when increasing speed by 1 kt the airflow over the wings reaches the speed of sound and the wing would also start to stall. Of course the point where the two of them get too close together (where insufficient margin exists) is above the maximum allowed altitude for the current conditions. This point is sometimes refered to as “the coffin corner”.
The below example is not specifically for the Airbus, but principles are the same. You can see that climbing at a lower speed and / or higher Mach causes a higher crossover altitude compared to climbing at higher speed and / or lower Mach. In the example below, climb is performed at a lower CAS and lower Mach in comparison to the example descent profile, which flown at higher Mach, changing over to higher CAS.
This explains why while climbing the Airbus with 350 kts causing crossover at 25.500 ft while climbing at 300 kts causing crossover at 31.800 ft as @PZL104 explained above.
Edit: in the above graph only the Mmo is shown, I’ve added the Vmo to the graph using MS Paint to hopefully make it more clear  . You can see at lower altitudes the Vmo is the limiting factor, at higher altitudes Mmo becomes limiting.
. You can see at lower altitudes the Vmo is the limiting factor, at higher altitudes Mmo becomes limiting.
![]()